MindGraph: Introduction

I previously described some of the motivation and intentions behind what I’m now calling MindGraph. Accepting the idea that my mind can be modeled as a graph where the nodes are representative of concepts and the edges are representative of the connections between concepts, MindGraph is what I’m calling the attempt to implement that model in software. It should be mentioned that the software is still very much in the exploratory phases and much can change, but the fundamental ideas are solid.

There are two fundamental pieces of data that need to be tracked in the application. The first is, of course, the graph. The graph in MindGraph is an unlabeled, directed graph. It consists solely of uniquely identified nodes with edges represented as the pair of two nodes. The nodes are not labeled with concepts, and the edges are not labeled with weights. Concepts and weights are tracked in three external maps: a map from nodes to concepts; a map from concepts to nodes; a map from edges to weights. Note that the presence of the node-concept and concept-node maps imply a 1 to 1 relationship between a specific concept and that node. Additionally, internally concepts are represented as a series of bytes. These maps act as optimizations by providing fast lookups. The edge map in particular provides the ability for convenient updates of edge weights. I consider the graph and it’s lookup maps as a single fundamental piece of data.

Concepts as I define them have three kinds of relationships.

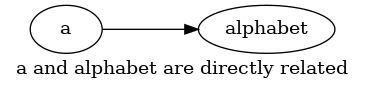A concept can be related to another concept directly. In the graph this is modeled as an edge between two nodes.

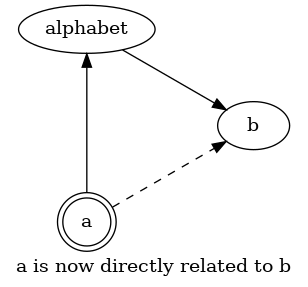
A concept can be related to another concept indirectly — modeled as two nodes connected through a single different node.

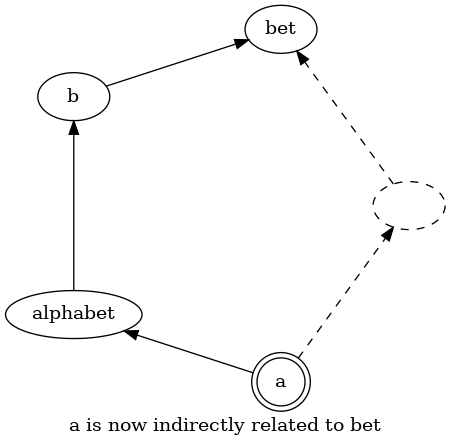
Finally a concept can be unrelated to another concept at all. In the graph two nodes that are connected through multiple other nodes are considered to be unrelated.

Intuition

The first algorithm I’ve implemented on the graph is designed to realize new connections between concepts and mimic intuition. The intuition algorithm starts with a single node and performs two main operations. The first operation is to find all of the nodes that are indirectly related to the starting node, then create an edge between each indirectly related node and the starting node. This makes the indirectly related nodes directly related. Each new direct relationship has a weight on its edge equal to sum of the weight of the two edges in the indirect relationship. This prevents any bias towards the new connection. This prevention of bias seems intuitively like the correct approach, however I haven’t clarified my reasoning behind it yet.

While the first portion of the intuition algorithm relates indirect concepts by making them directly related, the second portion of the algorithm takes unrelated concepts and relates them indirectly. For this I assume that any nodes that are unrelated by our definition must have some concept that relates them that hasn’t been discovered yet. I create this undiscovered concept by creating a new unlabeled node between the two unrelated concepts, and adding two edges. One between the starting node and the new node, and one between the new node and the unrelated node. This effectively makes them indirectly related, but through a concept the program doesn’t have name for yet.

The tertiary function of the intuition algorithm is shared by all other algorithms and operations on the graph. Every edge that is traversed while computing the algorithm is remembered and their weight is incremented. This is pretty similar to what happens in a neural network with the weighting of connections between neurons, and serves a similar function. Manipulating the weighting between connections influences how those connections are traversed. The higher the weight, the more likely that connection is used.

Learning

The intuition algorithm leaves the graph in a state where there are potentially many unlabeled nodes. An unlabeled node can’t be discussed or reasoned about directly. It can only be considered as the aggregate of its relationships to other nodes. While this is essential to form the basis of intuition, it is desirable to be able to talk about these unlabeled nodes. To this end an algorithm needs to be devised to handle this process.

One possible approach is to, given an arbitrary starting node, look at each directly related node and determine if any two nodes are representative of the same concept. The problem then becomes to define that equality. It’s most likely that a statistical determination will be necessary. This would take into account the direct connections on two nodes, along with their weights, and reduce them to a single value. If the two node values are within a certain margin of error then they can be considered to represent the same concept. The margin of error is a value that will certainly require manual tuning, and will probably also become necessary to have it determined at run time.

Self-Knowledge

The final point of consideration is this: It is at some point going to be desirable that the software involved in creating and running a MindGraph be represented within MindGraph itself. The reasoning behind this is simple. If MindGraph is to be a model of my mind and I contain a representation of the code of MindGraph in my mind, then it must be able to contain its own code, otherwise it is incomplete. At that point it becomes possible for MindGraph to be self-modifying. This naturally opens up the door for recursive self-improvement, a concept many believe is essential to the creation of a super-intelligence. I’ve done some research into representations of the lambda calculus as an abstract syntax tree and the translation of the reduction operations to that representation. An AST is a specialization of a graph, and the lambda calculus can represent any computable function, so it is possible if not straightforward to represent MindGraph within MindGraph.

This concludes my brief introduction to the internals of MindGraph. I should note that as of this article’s writing only the intuition algorithm is completed. In my next article I’ll go over some of the ideas behind input and output processing in MindGraph.